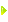一次方程应用题的六大类型，总结太全面了，难怪学霸都不看课本

【来源：易教网 更新时间：2025-02-28】

方程应用题是中考必考题型之一，但不少学生在这类题目上常常栽跟头。究其原因，主要是因为学生不了解这些题目的基本类型，没有掌握好每种类型的基本等量关系。因此，有必要详细介绍一次方程应用题的几个重要题型，希望能对那些在方程应用题上存在困难的同学有所帮助。

一、客房分配问题

这类问题通常涉及房间和客人之间的数量关系，通过设置合理的变量并根据已知条件列出方程来解决问题。例如，有一道经典的题目：“一房七客多七客，一房九客一房空”，即每个房间住7个人还多出7个人，而每个房间住9个人则会有一个房间是空的。我们设客房有x间，根据这两个相等关系可以列出方程：

\[ 7x + 7 = 9x - 9 \]

解这个方程，我们得到：

\[ 7x + 7 = 9x - 9 \]

\[ 7 + 9 = 9x - 7x \]

\[ 16 = 2x \]

\[ x = 8 \]

所以，共有8间客房。

接下来，假设每4人一个房间，需要16间客房，总费用为：

\[ 16 \times 20 = 320 \text{元} \]

如果定18间房，其中有四个人一起住，有三个人一起住，则总费用为：

\[ 18 \times 20 = 360 \text{元} \]

但实际上，由于有打折优惠，实际支付费用为：

\[ 18 \times 20 \times 0.8 = 288 \text{元} \]

比较两种方案，显然选择18间房更合算。

二、打折销售问题

打折销售问题是一次方程应用题中常见的题型之一，涉及到的量有标价、销售价、进价、折扣、利润率、利润等。它们之间的关系为：

- 售价 - 进价 = 利润

- 标价 × 折扣率 = 售价

- 进价 × 利润率 = 利润

以一道具体题目为例：某商品标价为100元，打八折后售价为80元，已知利润率为20%，求该商品的进价。

设进价为x元，根据等量关系列方程：

\[ 80 - x = 0.2x \]

\[ 80 = 1.2x \]

\[ x = \frac{80}{1.2} \]

\[ x = 66.67 \]

所以，该商品的进价为66.67元。

三、鸡兔同笼问题

鸡兔同笼问题是数学中非常典型的应用题，解题的关键在于理清题意，找出等量关系，列出符合要求的方程。例如，有大和尚和小和尚共100人，分得馒头共100个。大和尚一人分3个，小和尚3人分1个。问大和尚和小和尚各有多少人？

设大和尚有x人，小和尚有（100-x）人。根据题意，列出方程：

\[ 3x + \frac{100 - x}{3} = 100 \]

解这个方程：

\[ 9x + 100 - x = 300 \]

\[ 8x = 200 \]

\[ x = 25 \]

所以，大和尚有25人，小和尚有75人。

四、工程问题

工程问题的基本等量关系是：工作效率 × 工作时间 = 工作总量。此外，还可能涉及计划数量、超额百分数、实际完成百分数等。例如，某工厂计划生产一批产品，原计划每天生产100件，但由于技术改进，每天实际生产120件，提前5天完成了任务。问这批产品的总数量是多少？

设这批产品的总数量为x件，原计划时间为y天。根据题意，列出方程组：

\[ 100y = x \]

\[ 120(y - 5) = x \]

将两个方程联立解得：

\[ 100y = 120(y - 5) \]

\[ 100y = 120y - 600 \]

\[ 20y = 600 \]

\[ y = 30 \]

代入第一个方程：

\[ x = 100 \times 30 = 3000 \]

所以，这批产品的总数量为3000件。

五、征文比赛问题

这类问题通常涉及多个年级或多个群体的数量关系，通过设定适当的变量并列出方程来解决。例如，某学校举办征文比赛，七年级和八年级共收到118篇征文，其中七年级收到的征文篇数比八年级的一半还少2篇。问七年级和八年级各收到多少篇征文？

设七年级收到的征文篇数为x篇，八年级收到的征文篇数为y篇。根据题意，列出方程组：

\[ x + y = 118 \]

\[ x = \frac{y}{2} - 2 \]

将第二个方程代入第一个方程：

\[ \frac{y}{2} - 2 + y = 118 \]

\[ \frac{3y}{2} = 120 \]

\[ 3y = 240 \]

\[ y = 80 \]

代入第二个方程：

\[ x = \frac{80}{2} - 2 = 38 \]

所以，七年级收到38篇征文，八年级收到80篇征文。

六、物资调运问题

物资调运问题通常涉及多个仓库和多个目的地之间的运输安排，通过合理设置变量并列出方程来解决。例如，甲仓库和乙仓库分别向A港口和B港口调运物资，已知甲仓库向A港口调运x吨物资，向B港口调运y吨物资；乙仓库向A港口调运m吨物资，向B港口调运n吨物资。运输总费用为：

\[ z = ax + by + cm + dn \]

其中a、b、c、d分别为不同路线的单位运费。根据题意，列出不等式组，确定x、y、m、n的取值范围，并求出最小费用。

首先，根据调运方案用表示出从甲仓库运往B港口的物资的吨数，以及从乙仓库运往A、B两港口的物资吨数。然后，根据运输的总费用等于四条运输路线的费用总和，便可求出总费用（元）与（吨）之间的函数关系式。最后，根据问题的实际意义列出不等式组，即可求得的取值范围。

一次方程应用题虽然看似复杂，但只要掌握了不同类型题目的基本等量关系，理解题意并合理设置变量，列出方程，便能轻松解决。无论是客房分配、打折销售、鸡兔同笼、工程问题、征文比赛还是物资调运，关键在于找到能够反映题目全部含义的一个或两个相等关系。

通过不断练习，熟悉常用的数学语言，包括文字语言、符号语言、表格语言和图形语言之间的转化，才能在考试中游刃有余。

希望以上内容能帮助大家更好地理解和掌握一次方程应用题的解题方法，提高解题能力。